現代経済学応用:第12回講義ノート
2012年7月3日 火・3[新]現代経済学応用A[旧]ミクロ経済学A
第12回 展開形ゲーム(5)信念形成と完全ベイジアン・ナッシュ均衡
<今日の内容>
1 今日の問題意識
2 ベイズ・ルール
3 完全ベイジアン・ナッシュ均衡
1 今日の問題意識
※練習問題11.2
P2の情報集合上の信念 (p, 1-p) が,ある範囲でなければ,元のゲームのナッシュ均衡点は逐次合理的とはならない。
■Q. 信念形成の仮説は?その仮説の逐次合理性との両立は可能であろうか。
2 ベイズ・ルール
●先験確率(事前確率,prior probability)
●事後確率(posterior probability)
●ベイズ・ルール(Bayes' Rule)
3 完全ベイジアン・ナッシュ均衡
[信念形成仮説]
(B.1) 事前確率が正となっている情報集合 → ベイズ・ルールにて信念形成
(B.2) 事前確率がゼロとなっている情報集合 → 任意の信念
■Q. 下記例において,(B.1),(B.2) をどのように使うのか?
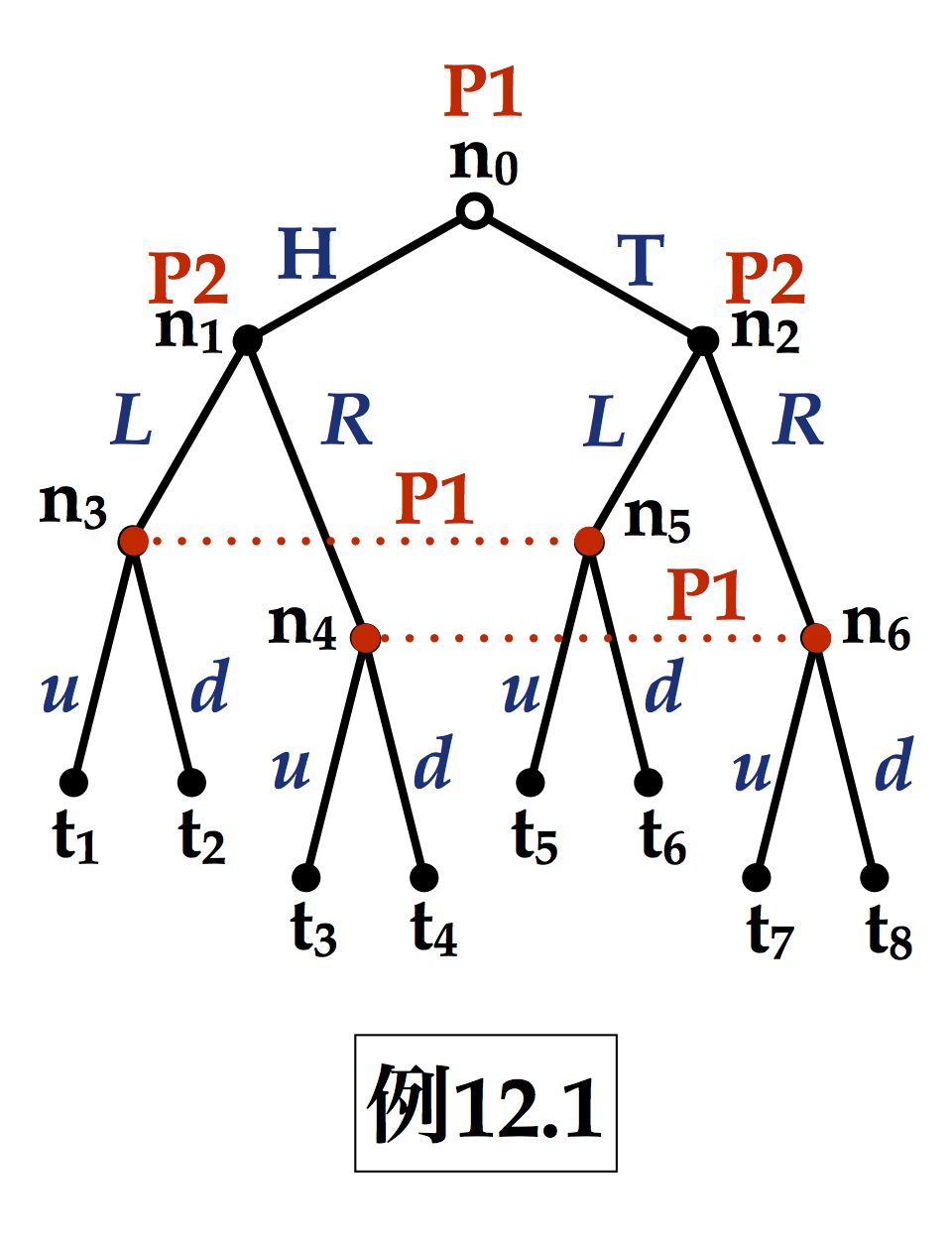
●完全ベイジアン・ナッシュ均衡(Perferct Bayesian Nash Equilibrium)
[条件1]逐次合理性
[条件2](B.1), (B.2) に基づく信念形成