現代経済学応用:第11回講義ノート
2012年6月26日 火・3[新]現代経済学応用A[旧]ミクロ経済学A
第11回 展開形ゲーム(4)逐次合理性と部分ゲーム完全性
<今日の内容>
1 今日の問題意識
2 信憑性のない脅し
3 逐次合理性
4 逐次合理性と部分ゲーム完全性の関係
1 今日の問題意識
[第8回問題意識]
■Q1. 一般に,プレイヤーの行動やタイプについての情報を,どのようにモデル化すれば良いであろうか。
■Q2. モデル化できたとして,どのような解概念が想定できるであろうか。支配可解性やナッシュ均衡といった解概念を導入するには,どのようにすれば良いであろうか。
■Q3. これまでの解概念を導入できたとしても,戦略形ゲームと異なって,何かしらの問題点は伴わないのであろうか。
[前回,今回]⇒ Q3
2 信憑性のない脅し
[第9回講義]
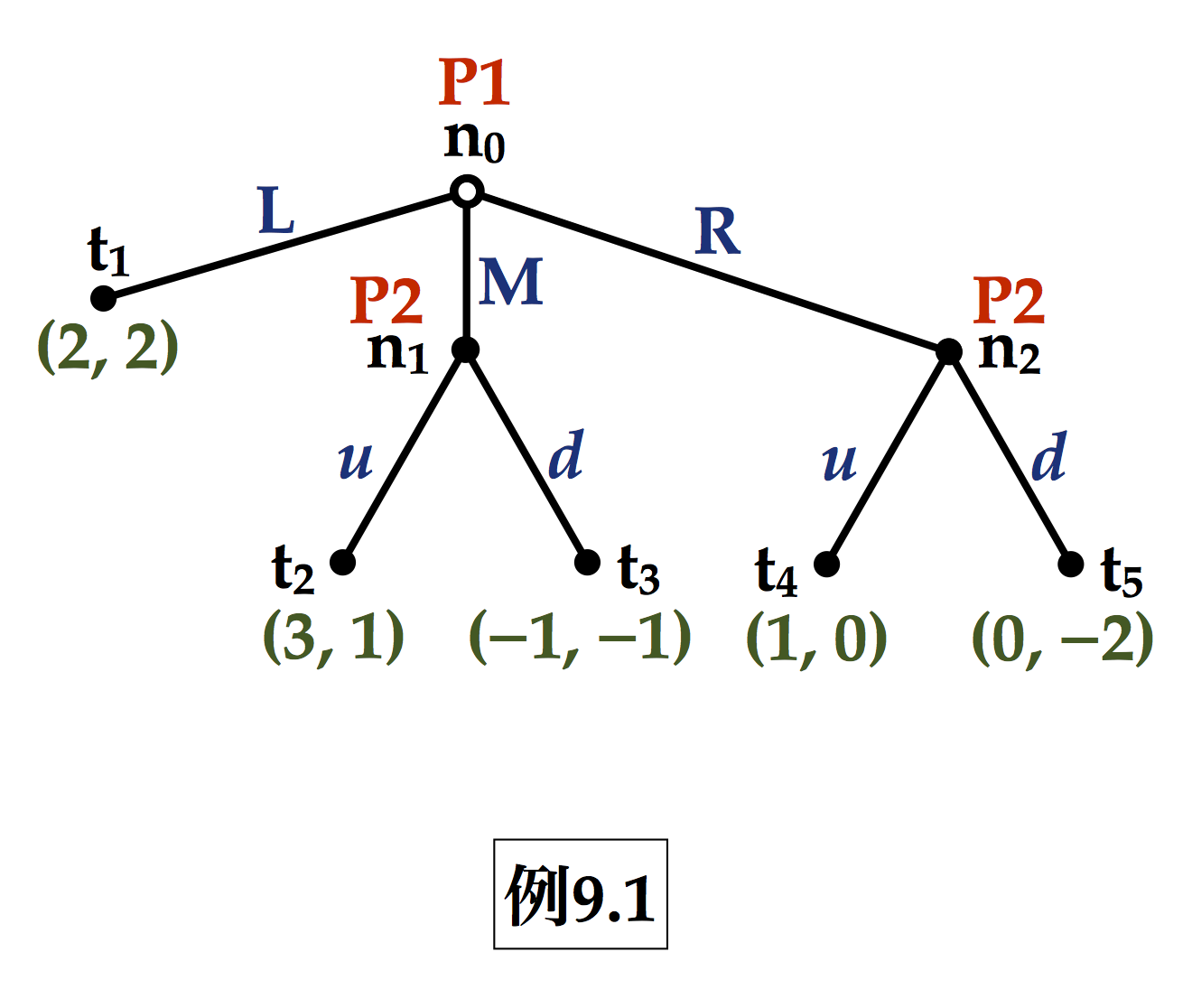
ナッシュ均衡点
例9.1)(M, (u, u)), (M, (u, d)), (L, (d, u)), (L, (d, d))
→ P2の (u, u) は,他の行動戦略を弱支配
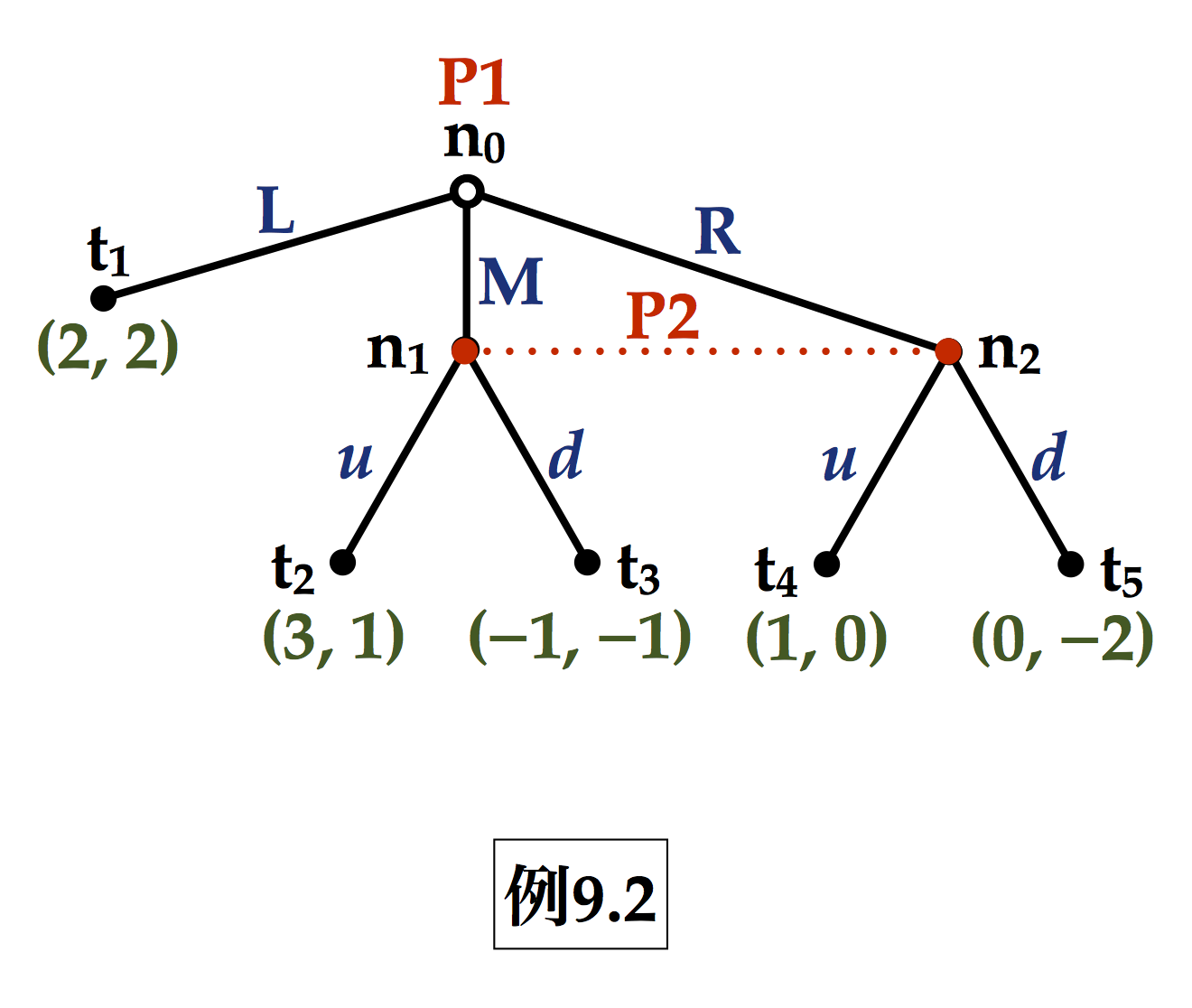
例9.2)(M, u), (L, d)
→ P2の u は,d を弱支配
■Q. 例9.2の場合,(M, u) 以外のナッシュ均衡点は,なぜ,ナッシュ均衡点になったのであろうか。
●信憑性のない脅し(Incredible Threat)
■Q. 例9.1の場合は,部分ゲーム完全性によって,(M, (u, u)) 以外のナッシュ均衡点は排除。ところが,例9.2の場合,部分ゲームは,全体ゲームのみである。どのようにすれば「信憑性のない脅し」に支えられたナッシュ均衡点を取り除けるのか。
3 逐次合理性
●信念(Belief)
●逐次合理性(Sequential Rationality)
●自然(偶然手番)
4 逐次合理性と部分ゲーム完全性の関係
[ファクト11.1]完全情報の展開形ゲーム
部分ゲーム完全性 = 逐次合理性