マクロ経済学:第27回講義ノート
2012年12月4日 火・1[新]マクロ経済学B[旧]現代経済学応用B
後期第12回 ニュー・クラシカル (5) 景気循環
<今日の内容>
1 実物景気循環論(リアル・ビジネスサイクル理論)
1 実物景気循環論(リアル・ビジネスサイクル理論)
モデルの構成
- ラムゼー・モデル(離散時間版)⇒ 前回講義
- 実物ショック
- 技術ショック
- 選好ショック
- 合理的期待
※ 以下では,技術ショックのみと単純化
技術ショック
[例27.1]コブ・ダグラス型生産関数
Yt = AtKtαNt1−α (0 < α < 1)
⇒
yt = Atktα
At:技術水準 ⇒ 確率変数
[例27.2]ランダム・ウォーク
log At+1 = μ + log At + ε
ε:平均0,分散σ2
消費者の選択
[ファクト27.1]最適消費計画の1階条件(不確実性あり)
u'(ct) = βEt{(1+rt+1)u'(ct+1)}
生産者の選択
[ファクト27.2]利潤最大化の1階条件(前回講義 ファクト26.3)
f'(kt) = rt + δ
生産物市場の均衡
●労働人口成長率ゼロのときの生産物市場の需給均衡
yt = ct + kt+1 - (1-δ)kt
厚生経済学の第1基本定理
●パレート効率性
[ファクト27.3]労働人口成長率をゼロとする。パレート効率な資源配分は,次のベルマン方程式の解である。
Vt(kt) = max{u(ct) + βEt[Vt+1(kt+1)]}
ただし,
kt+1 = yt - ct + (1-δ)kt
[ファクト27.4]厚生経済学の第1基本定理
労働人口成長率をゼロとする。このとき,
市場均衡(消費者,生産者,市場の一般均衡)での資源配分は,パレート効率
例証:u(c) = log c, y = Akα, δ = 1 の場合
[解]
ct = (1−αβ)yt
kt+1 = αβyt ・・・(※)
Vt(k) = (1-αβ)-1[αlog(k) + (1-β)-1{(1-αβ)log(1-αβ) + (αβ)log(αβ)} + Et{log(At) + βlog(At+1) + β2log(At+2) +・・・}]
- 一人当たり経済成長率(労働生産性の上昇率:
Δy/y = log yt - log yt-1)の長期的トレンドと変動
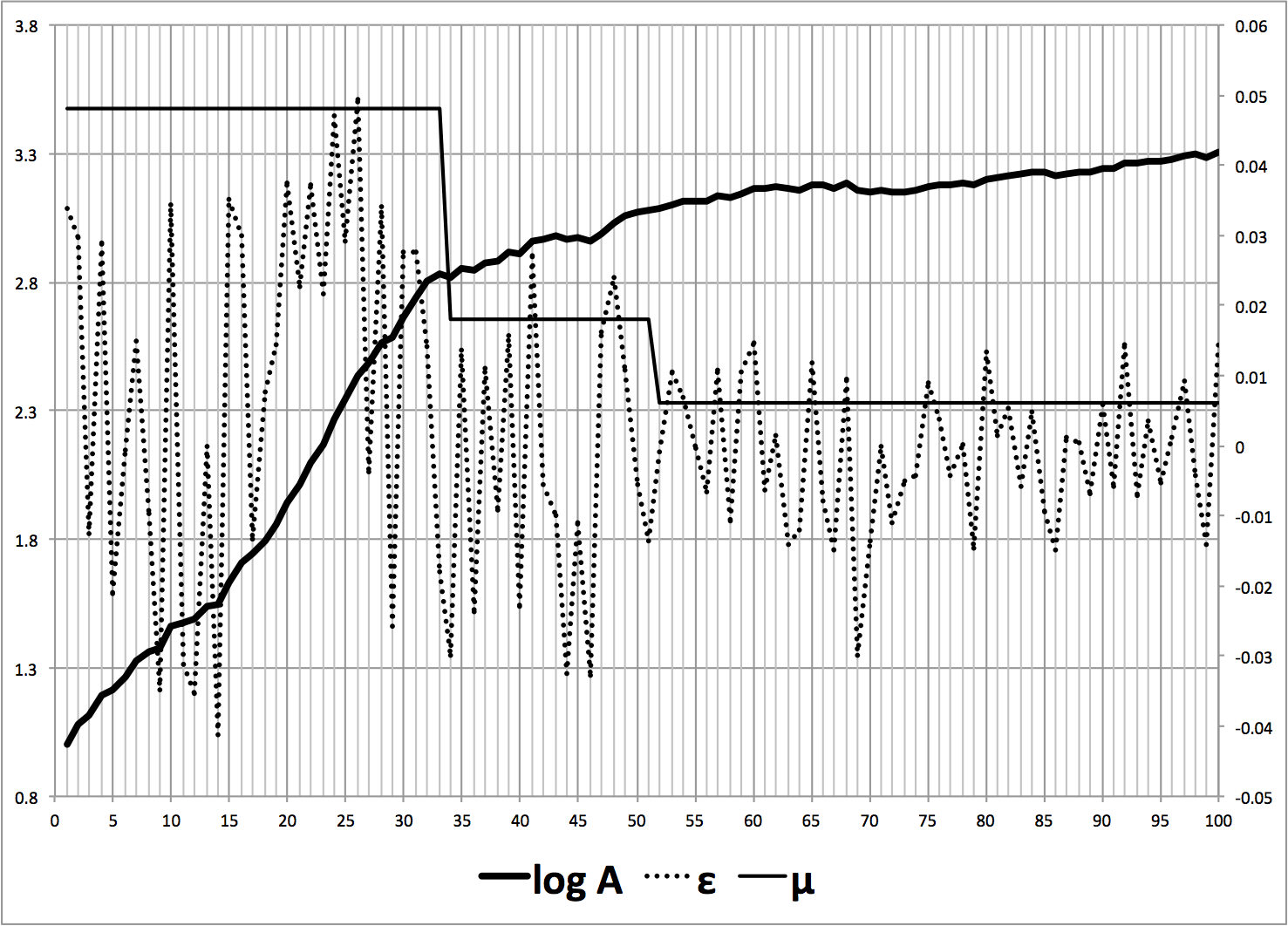
例27.2 ⇒Δy/y = (μ + ε)/(1 - α)⇒ ランダム・ウォーク - シミュレーション例:1955〜2030
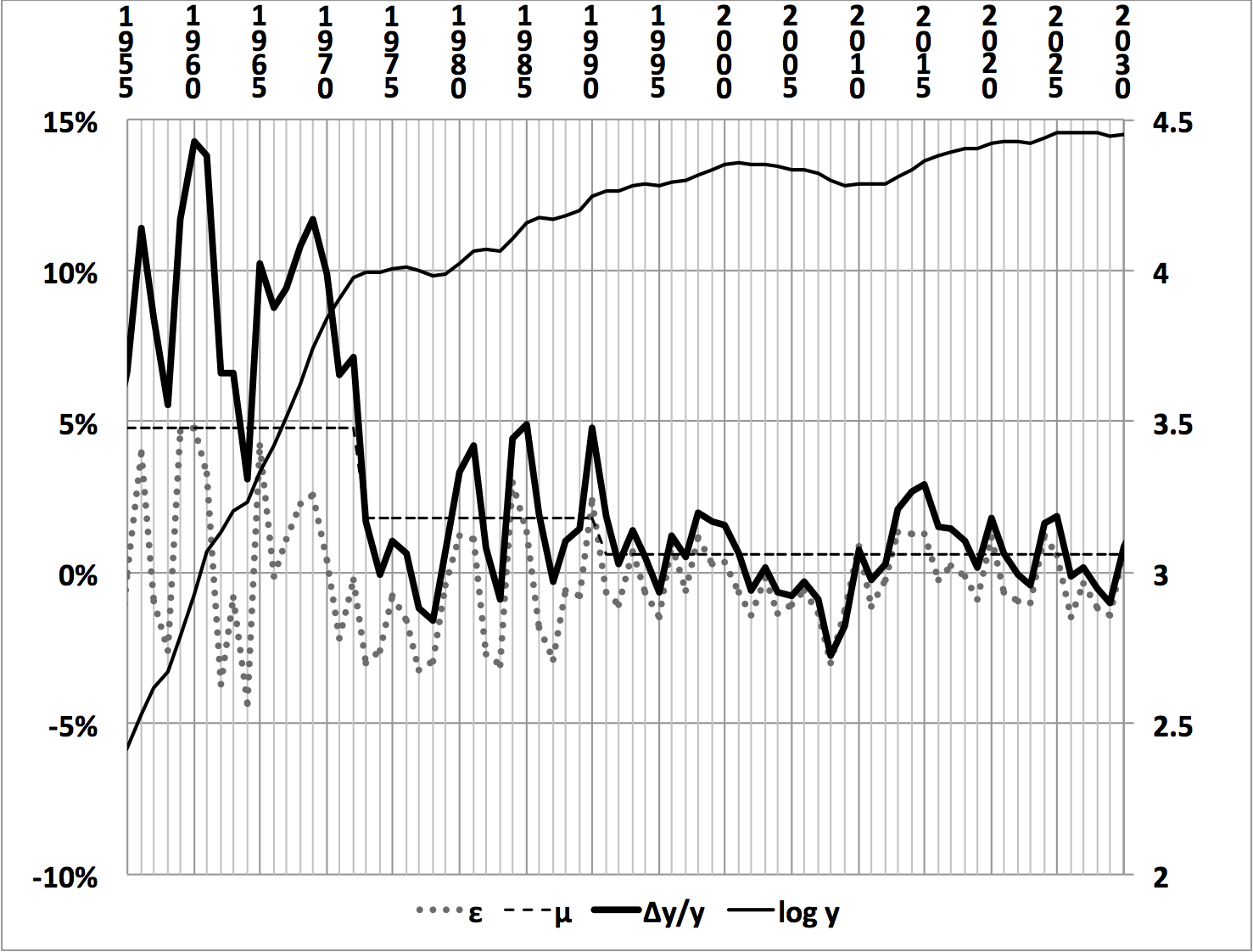
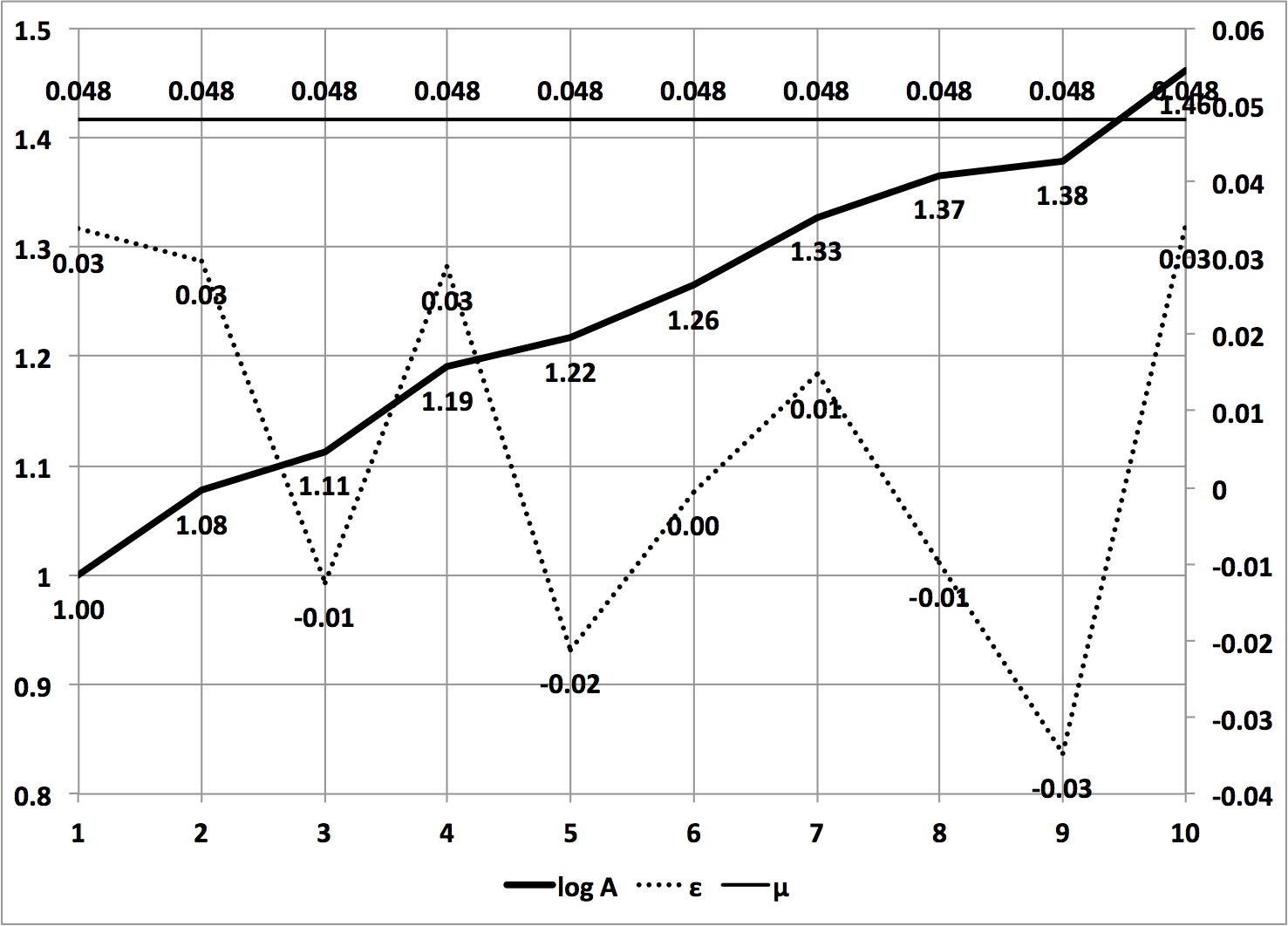
- 日本の実際のデータ:1955〜2010