現代経済学応用:第4回講義ノート
2012年5月1日 火・3[新]現代経済学応用A[旧]ミクロ経済学A
第4回 戦略形ゲーム(3)定和ゲームの解とミニマックス定理
<今日の内容>
1 今日の問題意識
2 マックスミニ,ミニマックス,ゲーム値
3 混合戦略とミニマックス定理
1 今日の問題意識
●定和ゲーム(Constant-Sum Game)
●ゼロ和ゲーム(Zero-Sum Game)
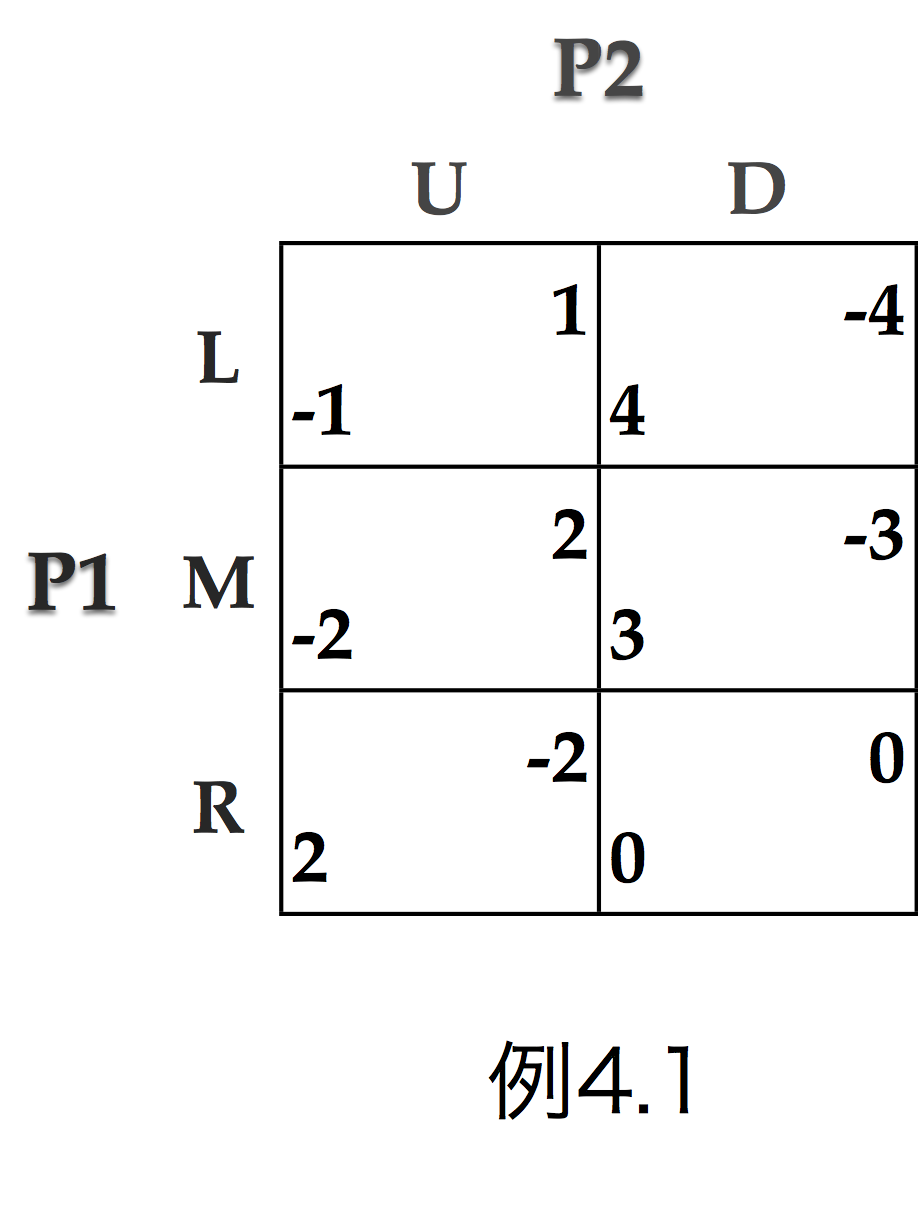
■Q. ジャンケンや例3.1,練習問題3.1,例4.1のような「ゼロ和ゲーム」での解は?
2 マックスミニ,ミニマックス,ゲーム値
●マックスミニ戦略とマックスミニ値(マキシミン,maximin)
●ミニマックス戦略とミニマックス値(minimax)
[例]例3.1, 練習問題3.1
●ゲーム値(ゲームの値,Game Value)
[ファクト4.1]ゲームが支配可解であれば,
(1) ゲーム値は定まり,
(2) 弱被支配戦略の繰り返し削除によって残る戦略の組は,P1のマックスミニ戦略とP2のミニマックス戦略の組に一致する。
3 混合戦略とミニマックス定理
■Q. 例4.1は,支配可解ではない。しかも,マックスミニ値とミニマックス値が異なる。こういう場合は?
●純戦略(純粋戦略,Pure Strategy)vs. 混合戦略(Mixed Strategy)
●期待利得,期待損失
<例4.1>
・P1の混合戦略:(p, 1-p)
・P1の期待利得
P2が U を選択したとき:p・(-1) + (1-p)・2 = 2 - 3p
P2が D を選択したとき:p・4 + (1-p)・0 = 4p
・マックスミニ値の導出
p = 2/7,P1の期待利得=8/7
・P2の混合戦略:(q, 1-q)
・P2の期待損失
P1が L を選択したとき:q・(-1) + (1-q)・4 = 4 - 5q
P2が R を選択したとき:q・2 + (1-q)・0 = 2q
・ミニマックス値の導出
q = 4/7,P2の期待損失=8/7
[定理4.1]ミニマックス定理
有限2人ゼロ和ゲームにおいて混合拡大すれば,マックスミニ値とミニマックス値は一致する。