ミクロ経済学:第10回講義ノート
2014年6月17日 火・3[新]ミクロ経済学A[旧]現代経済学応用A
消費者 (3) 消費者のジレンマ:予算制約内効用最大化
- [今回の内容]
- 1 予算制約
- 2 消費者の選択
- 3 需要関数
- [今日の問題意識]
- 序数的効用のときに,消費者はどのように選択するのであろうか。それには,何かしらの法則があるのであろうか。そこから需要価格を導出することは可能なのであろうか。
- [キーワード]
- 予算制約,予算制約線,相対価格(価格比),予算制約内効用最大化,最適消費計画,最適消費計画の1階条件,需要価格,需要量,普通需要関数,マーシャル需要関数,普通需要曲線
- [参考書]
- 奥山 3章 3.3節,3.4節 (3.4.1)
1 予算制約
【考えてみよう!】(参考書 練習問題3.14より)
カレー (商品X) とライス (商品Y) の量を自由に選べるカレー専門店を想像しよう。カレー1スクープ900円,ライス1スクープ50円,予算1,200円の時,選択可能な消費計画を図示してみよう!
●予算制約式(Budget Constraint)
$p_X x + p_Y y \leqq I$
$p_X$::商品Xの市場価格
$p_Y$:商品Yの市場価格
$I$:予算
●予算制約線
[$x$軸] [$y$軸] [勾配]
●相対価格(Relative Price),価格比
2 消費者の選択
●予算制約内効用最大化
(M) $\max_{x,y} U = u(x,y)$
s.t. $p_X x + p_Y y \leqq I$
●最適消費計画
[ファクト10.1](最適消費計画の1階条件)最適消費計画では,
$MRS = \frac{p_X}{p_Y}$
需要価格の導出
●需要価格【復習】
3 需要関数
【考えてみよう!】
最大化問題 (M) での選択対象の変数は,何であろうか?一方,所与となっている変数は,何であろうか?
●需要量
●普通需要関数 (マーシャル需要関数)
●普通需要曲線
【求めてみよう!】
太郎さんと花子さん(前々回講義)の各々について,商品Xの普通需要曲線を求めてみよう!
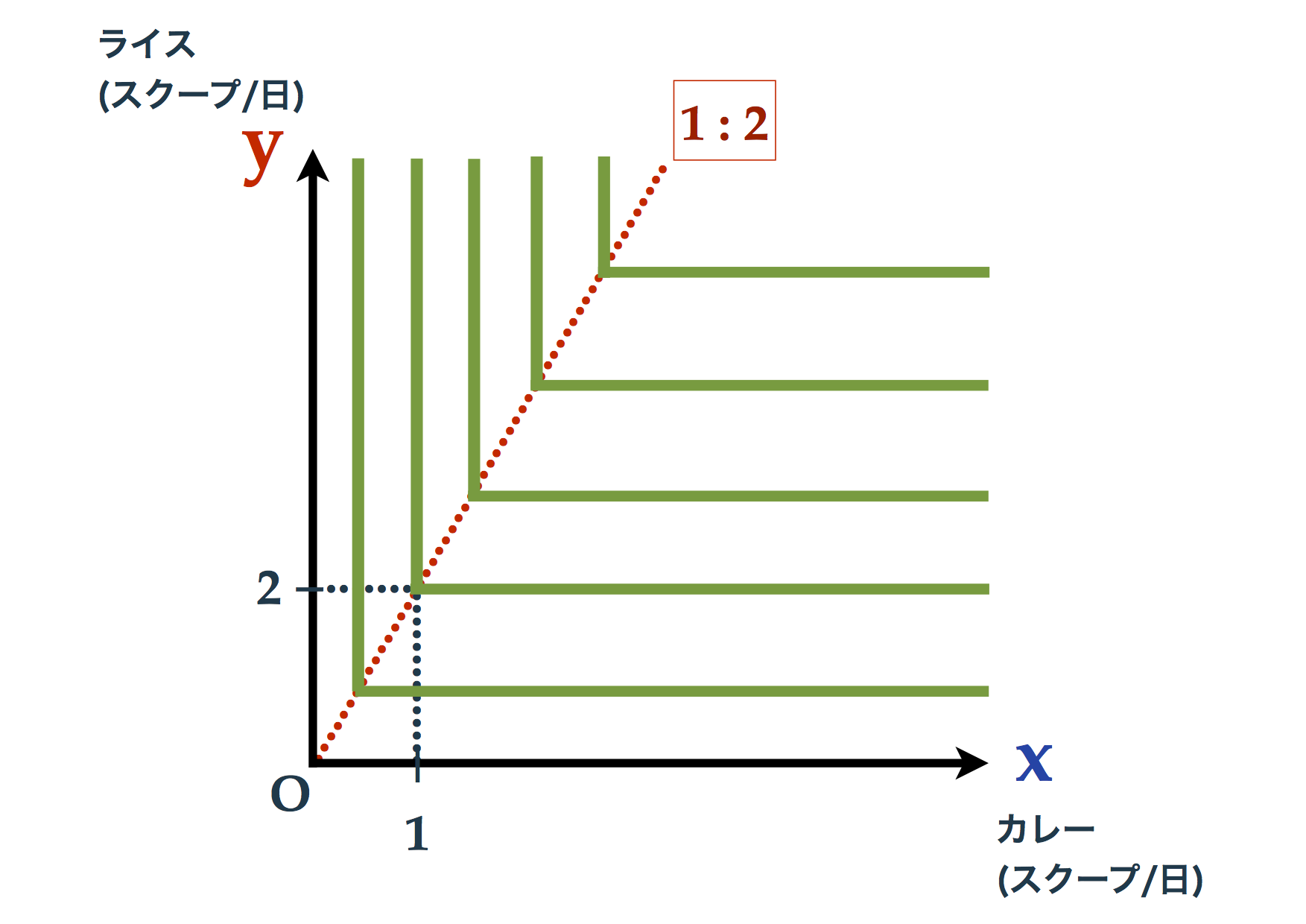
<無差別曲線群>
【太郎さん】
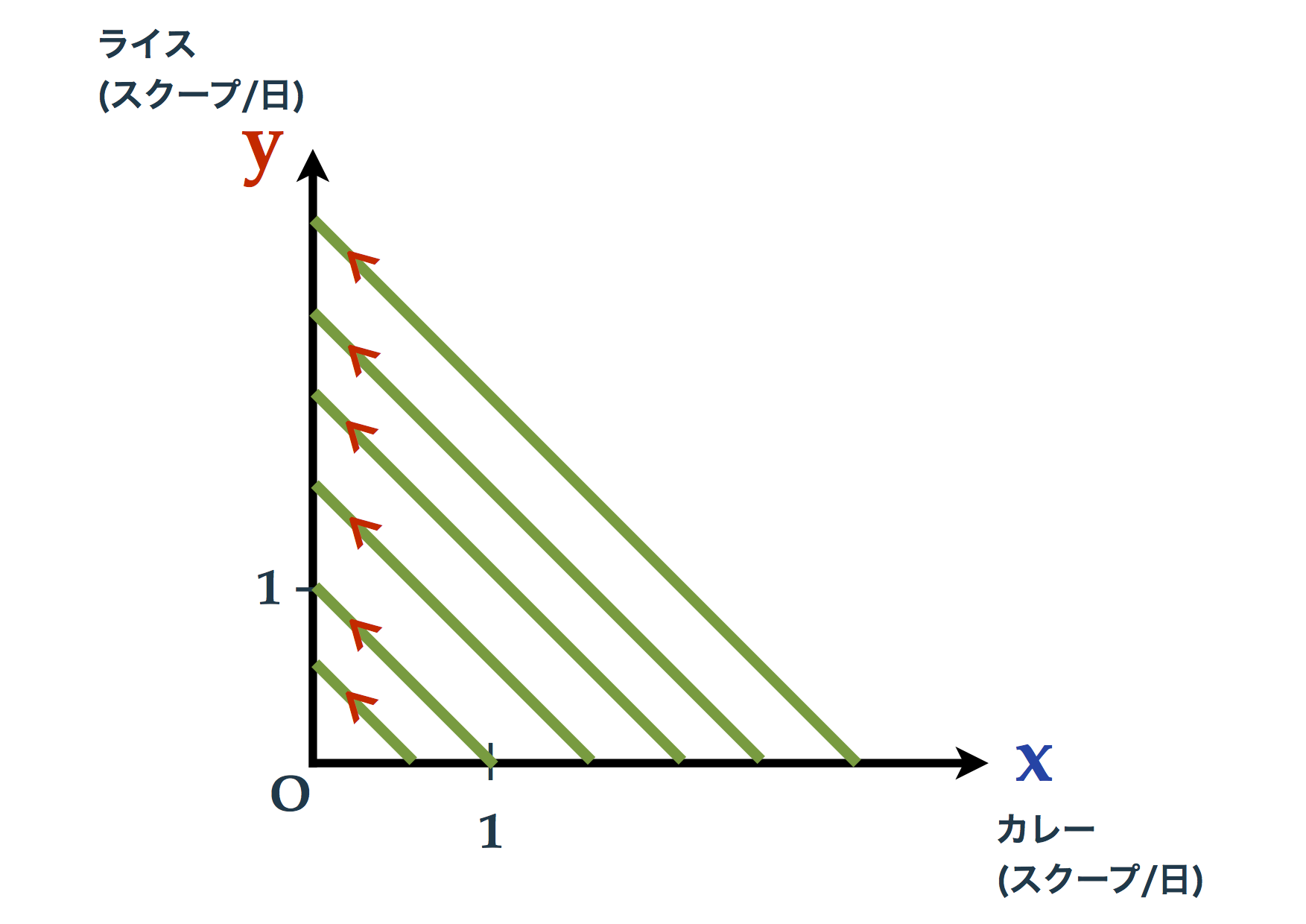
【花子さん】